Lançamento horizontal (sem rotação)

ATENÇÃO: se você é aluno de alguma disciplina de laboratório de física básica do Departamento de Física da UFSC (FSC 5122, FSC 5141 etc.) e o relatório que você deve apresentar é parte do processo avaliativo da disciplina, você deve seguir as instruções no final desse roteiro. Se não, divirta-se como quiser!
− 0,80 m − 0,20 m
m

rastro

Um taco (bloco vermelho) é posicionado a uma certa distância de um alvo (bloco preto). O taco move-se em movimento retilíneo uniformemente variado com velocidade inicial nula e aceleração constante, até atingir o alvo.

O bloco e o alvo têm as mesmas dimensões e massas e movem-se sem atrito e sem girar pela superfície da mesa. Ao colidir com o alvo, a energia e o momento linear do taco são transferidos integralmente para o alvo (colisão perfeitamente elástica).

A posição em que o alvo atinge o chão é definida pela velocidade final do taco ao colidir com ele e da altura da superfície em que estão em relação ao chão. A posição em que o bloco para no chão é definida pela sua velocidade (horizontal) e o coeficiente de atrito entre o bloco e o solo.

O objetivo do experimento é determinar:

  1. a aceleração $a_t$ do taco;
  2. a altura de lançamento $y_0$ do bloco alvo.

Para entender como isso pode ser feito, considere a figura a seguir.

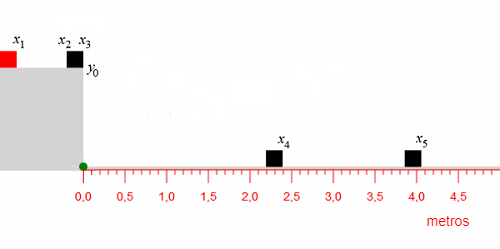
A origem do sistema de coordenadas está na "borda do precipício" ($x_3 = 0{,}00$ m) na direção $x$ e "no chão" na direção $y$ ($y_0$ é a altura de lançamento do bloco), representada pelo ponto verde.

O taco parte do repouso de um ponto $x_1$ escolhido pelo usuário (entre −0,80 m e −0,20 m da origem) e move-se com aceleração uniforme (não conhecida do usuário) até colidir com o alvo em $x_2$ = −0,20 m.

O taco e o alvo têm massas e tamanhos iguais (0,20 m de largura) e a colisão é perfeitamente elástica, de modo que o alvo parte com a mesma velocidade que o taco tem no momento da colisão.

O ponto de partida do alvo é $x_3$ = 0,00 m. O alvo toca o solo em $x_4$. Ao longo do "vôo" não há rotação ou perda de energia por atrito com o ar. Ao tocar o solo, assumimos que o alvo perde toda energia cinética correspondente à contribuição da componente $y$ da velocidade, que passa a ser nula, permanecendo inalterada a velocidade na direção $x$. A partir desse ponto o bloco move-se sobre o chão, com atrito. A força de atrito é conhecida e provoca uma aceleração de (−5,0 ± 0,2) m/s2 no bloco.

A velocidade $v_t$ com que o taco atinge o alvo (e que o alvo carregará integralmente), partindo do repouso ($v_{0t} = 0,00$ m/s) é dada por:

$$ v_t^2 = v_{0t}^2 + 2 a_t (x_2 - x_1) $$ $$ v_t = \sqrt{ 2 a_t (x_2 - x_1) } $$ $$ v_t = \sqrt{ 2 a_t {\Delta x}_t } $$

onde ${\Delta x}_t = x_2 - x_1$ é um valor conhecido, determinado pelo usuário, e $a_t$, a aceleração do projétil, que é uma das grandezas procuradas.

A posição $x_4$ em que o bloco toca o solo ($y = 0,00$ m) pode ser obtida calculando-se o tempo de queda $t_q$ partindo de $y_0$ com velocidade $v_{0y} = 0{,}00$ m/s, sujeito à aceleração da gravidade $g$, e utilizando o resultado na equação para o movimento retilíneo uniforme na direção $x$. Lembrando que $x_3 = 0{,}00$ m e assumindo uma colisão totalmente elástica, de modo que a velocidade $v_p$ do projétil seja igual à velocidade $v_t$ do taco no momento da colisão, obtemos:

$$ y = y_0 + v_{0y} t - \frac{g t^2}{2} $$ $$ t_q = \sqrt{ \frac{2y_0}{g} } $$ $$ x_4 = x_3 + v_p t_q $$ $$ x_4 = \sqrt{ 2 a_t {\Delta x}_t } \sqrt{ \frac{2y_0}{g} } $$

Essa expressão pode ser rearranjada para explicitar a dependência de $x_4$ (mensurável) com ${\Delta x}_t$ (mensurável):

$$ x_4 = \sqrt{ \frac{4 a_t y_0}{g} } \sqrt{{\Delta x}_t} $$

Rearranjando a expressão, podemos obter o valor de $y_0$:

$$ y_0 = \frac{x_4^2 g}{4 a_t {\Delta x}_t} $$

Não é possível calcular o valor de $y_0$ pois não temos o valor da aceleração $a_t$ do taco. Para obtê-la, precisamos de mais informações, e a medida de $x_5$ e o conhecimento da desaceleração devida à força de atrito vêm a calhar.

Assumimos que em $x_4$ (o ponto em que o alvo toca o solo) sua velocidade horizontal é igual à velocidade de lançamento $v_t$ (ainda desconhecida). Usando novamente a equação de Torricelli e considerando que a velocidade final $v_f = 0$, que a aceleração de frenagem $a_f$ é conhecida e que ${\Delta x}_f = x_5 - x_4$ pode ser medido, obtemos a aceleração $a_t$ do taco:

$$ v_f^2 = v_t^2 + 2 a_f (x_5 - x_4) = v_t^2 + 2 a_f {\Delta x}_f $$ $$ 2 a_t {\Delta x}_t = - 2 a_f {\Delta x}_f $$ $$ a_t = - a_f \frac{{\Delta x}_f}{{\Delta x}_t} = - a_f \frac{x_5 - x_4}{x_2 - x_1} $$

Se medirmos ${\Delta x}_f$ em função e ${\Delta x}_t$ podemos construir um gráfico cujo coeficiente angular é a razão $-a_t/a_f$:

$$ {\Delta x}_f = - \frac{a_t}{a_f} {\Delta x}_t $$

Como $a_f$ é conhecido, podemos utilizar o coeficiente angular para calcular $a_t$.

Uma sugestão de procedimento experimental é a seguinte:

Carregue o aplicativo. Ao fazê-lo, ele sorteia valores para a aceleração do taco ($a_t$) e para a altura de lançamento ($y_0$), valores que você descobrirá analisando os dados.

Escolha 6 valores para $x_1$ e faça 3 medidas de $x_4$ e $x_5$ nessa condição ($x_2$ = −0,20 m e $x_3$ = 0,00 m são bem definidos). Note que $x_4$ não varia de lançamento para lançamento (por isso somente uma coluna), mas que $x_5$ varia devido a flutuações estatísticas do movimento com atrito (por isso três colunas). Ao final do processo você terá uma tabela conjuntos de valores ($x_1$, $x_2$, $x_3$, $x_4$, $x_5$) que podem ser rearranjados como (${\Delta x}_t$, ${\Delta x}_f$):

$x_1$
(m)		 $x_2$
(m)		 $x_3$
(m)		 $x_4$
(m)		 $x_5$
(m)		 $\bar{x}_5$
(m)		 ${\Delta x}_t$
(m)		 ${\Delta x}_f$
(m)
$x_1$
(m)		 $x_2$
(m)		 $x_3$
(m)		 $x_4$
(m)		 $x_5$
(m)		 $\bar{x}_5$
(m)		 ${\Delta x}_t$
(m)		 ${\Delta x}_f$
(m)

Os coeficientes linear $a$ e angular $b$ obtidos da regressão linear utilizando $x= \{{\Delta x}_{ti}\}$ e $y = \{{\Delta x}_{fi}\}$ são:

$$ a = (0{,}0 \pm 0{,}0) \,\, \text{m} $$ $$ b = (4{,}2 \pm 0{,}1) \,\, \text{(m/m, ou adimensional)} $$

Considerando que $a_t = b a_f$ e $a_f$ = (−5,0 ± 0,2) m/s2 obtemos $a_t$ = (21 ± 1) m/s2.

O valor da altura de lançamento $y_0$ também pode ser obtido ajustando uma reta aos dados experimentais:

$$ y_0 = \frac{x_4^2 g}{4 a_t {\Delta x}_t} $$ $$ x_4^2 = \frac{4 a_t y_0}{g} {\Delta x}_t $$

Os coeficientes linear $a$ e angular $b$ obtidos da regressão linear utilizando $x= \{{\Delta x}_{ti}\}$ e $y = \{x_{4i}^2\}$ são:

$$ a = (0{,}0 \pm 0{,}0) \,\, \text{m}^2 $$ $$ b = (7{,}9 \pm 0{,}1) \,\, \text{m} $$

Considerando que $y_0 = bg/4a_t$, $g$ = 9,80 m/s2 e o valor de $a_t$ calculado acima, obtemos $y_0$ = (0,92 ± 0,05) m.

Se você é aluno de alguma disciplina de laboratório de física básica do Departamento de Física da UFSC (FSC 5122, FSC 5141 etc.) você deve apresentar um relatório em um único arquivo PDF contendo:

  1. um cabeçalho com o código da disciplina, o nome da disciplina, o número da turma, o nome do professor responsável, o seu nome e o seu número de matrícula;
  2. um print-screen ou qualquer outra forma de registro da tabela com os dados adquiridos (conforme exemplo no texto); sem ela, não será possível avaliar o experimento e a nota será 0 (zero);
  3. um gráfico de $\Delta x_f$ em função de $\Delta x_t$, contendo legenda com informações sobre o ajuste realizado (conforme exemplo no texto);
  4. um gráfico de $(x_4)^2$ em função de $\Delta x_t$, contendo legenda com informações sobre o ajuste realizado (conforme exemplo no texto);
  5. apresentação do valor da aceleração do taco $a_t$, respectivo erro e unidade (conforme exemplo no texto);
  6. apresentação do valor da altura de lançamento $y_0$, respectivo erro e unidade (conforme exemplo no texto);